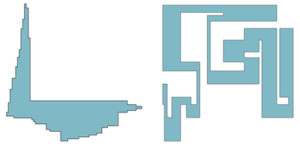
We developed a C++ library for creating orthogonal polygons and some subclasses (row-convex, column-convex, convex, path, and spiral orthogonal polygons), with a given number of vertices. The algorithms are based on the Inflate-Paste method [2], which generates grid orthogonal polygons (a.k.a. permutominoes). A grid orthogonal polygon is an orthogonal polygon without collinear edges, defined in a unit square lattice and that has exactly one edge on all the grid lines that intersect their minimum bounding square. The Inflate-Paste method constructs an n-vertex grid orthogonal polygon iteratively from a unit square in \(O(n^2)\) time and \(O(n)\) space. At each iteration, it applies two transformations (called Inflate and Paste) to glue a new rectangle to the previous grid orthogonal polygon, yielding a new grid orthogonal polygon with one more reflex vertex. We designed tailored versions of the Inflate-Paste algorithm to generate grid orthogonal polygons in the aforementioned subclasses. For the row-convex, column-convex and convex grid orthogonal polygons, the algorithm runs in \(O(n)\) time.
Generic orthogonal polygons are obtained from grid orthogonal polygons by sliding their edges while preserving their relative order (in a plane sweep). The sliding procedure is executed k times, where k is a user-defined parameter, running in \(O(n \cdot k)\) time, using \(O(n)\) space. The generator may create polygons with collinear edges. For that purpose, it performs a final transformation making use of another parameter that defines the probability of moving an edge to the same line of the previous one (if that is possible). This transformation runs in \(O(n^2)\) time.
The project uses CGAL::Arrangement_2 from the 2D Arrangements CGAL package, to have a DCEL as a possible representation for the generated orthogonal polygon. It is also possible to have as output a doubly linked list of vertices of type CGAL::Point_2 in counterclockwise order.
Publications
- C. L. Ferreira
Algorithms for Chromatic Art Gallery Problems with Vertex α-Guards
M.Sc. Thesis in Computer Science, Faculty of Sciences, University of Porto, 2016 [link][bibtex] - A. P. Tomás and A. L. Bajuelos
Quadratic-Time Linear-Space Algorithms for Generating Orthogonal Polygons with a Given Number of Vertices
In Laganá A. et al (Eds), ICCSA, LNCS, vol. 3045, pp. 117-126, 2004, Springer [link][bibtex]
