Many path-finding algorithms on graphs such as A* are sped up by using a heuristic function that gives lower bounds on the cost to reach the goal. Aiming to apply similar techniques to speed up sampling-based motion-planning algorithms, we use effective lower bounds on the cost between configurations to tightly estimate the cost-to-go. We then use these estimates in an anytime asymptotically-optimal algorithm which we call Motion Planning using Lower Bounds (MPLB). MPLB is based on the Fast Marching Trees (FMT*) algorithm recently presented by Janson and Pavone. An advantage of our approach is that in many cases (especially as the number of samples grows) the weight of collision detection in the computation is almost negligible with respect to nearest-neighbor calls. We prove that MPLB performs no more collision-detection calls than an anytime version of FMT*. Additionally, we demonstrate in simulations that for certain scenarios, the algorithmic tools presented here enable efficiently producing low-cost paths while spending only a small fraction of the running time on collision detection.
Experimental results*
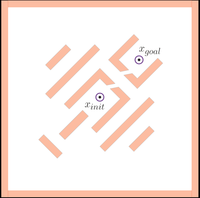
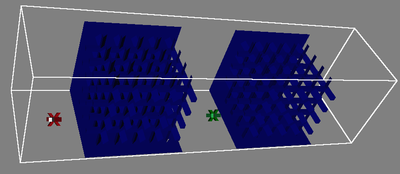
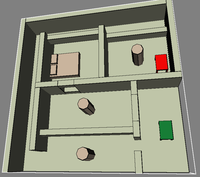
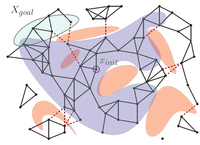
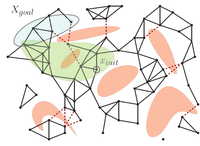
Benchmark scenarios. The start and goal configuration are depicted in green and red, respectively
|
|
|
|
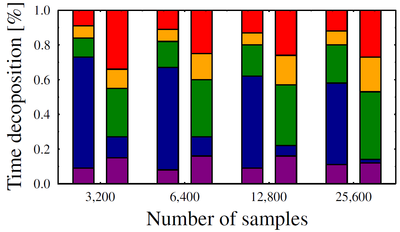
Percentage of time spent for each of the main components in each iteration for both algorithms.
Each iteration is represented by the number of samples used, the bars on the left (right) of each iteration represent the result of aFMT* (MPLB, respectively).
Note that the time of each iteration for each algorithm is different, the results are presented in percentages of the total running time for each algorithm.
|
|
|
* Implemented using OMPL, the cubicles scenario is provided with the OMPL distribution.