We introduce bindings that enable the convenient, efficient, and reliable use of software modules of CGAL (Computational Geometry Algorithm Library), which are written in C++, from within code written in Python. There are different tools that facilitate the creation of such bindings. We present a short study that compares three main tools, which leads to the tool of choice. The implementation of algorithms and data structures in computational geometry presents tremendous difficulties, such as obtaining robust software despite the use of (inexact) floating point arithmetic, found in standard hardware, and meticulous handling of all degenerate cases, which typically are in abundance. The code of CGAL extensively uses function and class templates in order to handle these difficulties, which implies that the programmer has to make many choices that are resolved during compile time (of the C++ modules). While bindings take effect at run time (of the Python code), the type of the C++ objects that are bound must be known when the bindings are generated, that is, when they are compiled. The types of the bound objects are instances (instantiated types) of C++ function and class templates. The number of object types that can potentially be bound, in implementation of generic computational-geometry algorithms, is enormous; thus, the generation of the bindings for all these types in advance is practically impossible. For example, the programmer needs to choose among a dozen types of curves (e.g., line segments, circular arcs, geodesic arcs on a sphere, or polycurves of any curve type) to yield a desired arrangement type; often there are several choices to make, resulting in a prohibitively large number of combinations. We present a system that rapidly generates bindings for desired object types according to user prescriptions, which enables the convenient use of any subset of bound object types concurrently. After many years, in which the usage of these packages was restricted to C++ experts, the introduction of the bindings made them easily accessible to newcomers and practitioners in non-computing fields, as we report in the paper.
Concepts-Binding Coupling
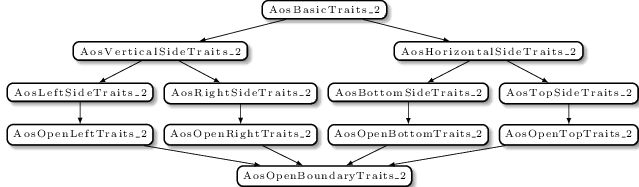
Generic programming enables the implementation of generic algorithms, which work on collections of different types, can be easily maintained, extended, and customized, and are type safe and easier to read. As mentioned in the introduction, CGAL rigorously adheres to the generic programming paradigm. As a consequence, most components of CGAL are either class or function templates. Many of the parameters of these templates are described in terms of models of concepts. When a class or a function template is instantiated, each one of its template parameters is substituted with a model of one or more concepts associated with the template parameter. Close to 750 concepts can be identified in CGAL at the time this article is written. Most hierarchy graphs of concepts are small. Few graphs, such as the graph of concepts of the geometry traits of the 2D Arrangements on Surfaces package, are quite large with intricate refinement relations. We use clusters of closely related concepts to describe the refinement relations among them; see, e.g., the open-boundary cluster of the 2D Arrangement on Surface traits concept in the figure above. We have introduced tight coupling between concepts and (i) binding generations and (ii) type annotation.
Software
The bindings software resides in a public git repository called CGAL Python Binding.
The Wiki page within provide detailed instructions for building the bindings and using them.
Supported Modules
| Package | Flag | Module |
|---|---|---|
| 2D Arrangements | ARRANGEMENT_ON_SURFACE_2 |
Aos2 |
| 2D Alpha Shapes | ALPHA_SHAPE_2 |
As2 |
| 3D Alpha Shapes | ALPHA_SHAPE_3 |
As3 |
| 2D Regularized Boolean Set-Operations | BOOLEAN_SET_OPERATIONS_2 |
Bso2 |
| Basic Viewer | BASIC_VIEWER |
Bvr |
| Bounding Volumes | BOUNDING_VOLUMES |
Bv |
| 2D Convex Hulls and Extreme Points | CONVEX_HULL_2 |
Ch2 |
| 3D Convex Hulls | CONVEX_HULL_3 |
Ch3 |
| Envelopes of Curves in 2D | ENVELOPE_2 |
Env2 |
| Envelopes of Surfaces in 3D | ENVELOPE_3 |
Env3 |
| 2D and 3D Geometry Kernel | KERNEL |
Ker |
| dD Geometry Kernel | KERNEL_D |
Kerd |
| Geometric Object Generators | GEOMETRIC_OBJECT_GENERATORS |
Gog |
| 3D Boolean Operations on Nef Polyhedra | NEF_3 |
Nef3 |
| 2D Polygons | POLYGON_2<c/ode> |
Pol2 |
| 3D Polyhedral Surfaces | POLYHEDRON_3 |
Pol3 |
| Polygon Mesh Processing | POLYGON_MESH_PROCESSING |
Pmp |
| 2D Polygon Partitioning | POLYGON_PARTITIONING |
Pp |
| 2D Minkowski Sums | MINKOWSKI_SUM_2 |
MS2 |
| dD Spatial Searching | SPATIAL_SEARCHING |
Ss |
| dD Spatial Sorting | SPATIAL_SEARCHING |
St |
| Surface Mesh | SURFACE_MESH |
Sm |
| 2D Intersections of Curves | SURFACE_SWEEP_2 |
Sw2 |
| 2D Triangulations | TRIANGULATION_2 |
Tri2 |
| 3D Triangulations | TRIANGULATION_3 |
Tri3 |
| 3D Triangulations | TRIANGULATION_3 |
Tri3 |
| dD Triangulations | TRIANGULATION_D |
Trid |
| 2D Visibility | VISIBILITY_2 |
Vis2 |
| Data last updated: July 2025 | ||
