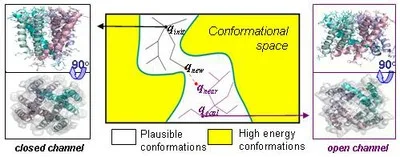
Proteins are active, flexible machines that perform a range of different functions, but experimental knowledge on protein molecular motion is still limited. We recently intoduced Rosetta PathRover, a general framework for the generation, alignment and comparison of pathways between two known protein conformations using is rooted in probabilistic motion-planning techniques in robotics, allows the efficient generation of collision-free motion pathways, while considering a wide range of degrees of freedom (dofs) involved in the motion. PathRover is innovative tthe Rapidly exploring Random Trees (RRT) algorithm, a motion prediction algorithm.
The PathRover framework hanks to the following features: (1) A general setup designed for the introduction of prior experimental data or expert intuitions into the RRT algorithm allows truncation of non-favorable branches and emphasis on relevant directions; (2) Integration into Rosetta (a leading framework for different modeling tasks) allows the use of state of the art energy function and conformational modeling; and (3) An efficient post-processing algorithm for the alignment and comparison of molecular motion pathways (similar to string matching algorithms) allows the hybridization of suboptimal pathways segments to construct optimal pathways. The framework can therefore complement slower molecular dynamics techniques. We used the framework to explore in detail molecular motions of domain swapping, Ion channels, and enzymes.

