We present a major revamp of the point-location data structure for general two-dimensional subdivisions via randomized incremental construction, implemented in CGAL, the Computational Geometry Algorithms Library. We can now guarantee that the constructed directed acyclic graph \(G\) is of linear size and provides logarithmic query time. Via the construction of the Voronoi diagram for a given point set \(S\) of size \(n\), this also enables nearest-neighbor queries in guaranteed \(O(\log n)\) time. Another major innovation is the support of general unbounded subdivisions as well as subdivisions of two-dimensional parametric surfaces such as spheres, tori, cylinders. The implementation is exact, complete, and general, i.e., it can also handle non-linear subdivisions. Like the previous version, the data structure supports modifications of the subdivision, such as insertions and deletions of edges, after the initial preprocessing. A major challenge is to retain the expected \(O(n \log n)\) preprocessing time while providing the above (deterministic) space and query-time guarantees. We describe efficient preprocessing algorithms, which explicitly verify the length \(L\) of the longest query path. However, instead of using \(L\), our implementation is based on the depth \(D\) of \(G\). Although we prove that the worst case ratio of \(D\) and \(L\) is \(\Theta(n / \log n)\), we conjecture, based on our experimental results, that this solution achieves expected \(O(n \log n)\) preprocessing time.
The Basic Algorithm
We review here the known random incremental construction (RIC) of an efficient point location structure. Given an arrangement of \(n\) pairwise interior disjoint \(x\)-monotone curves, a random permutation of the curves is inserted incrementally, constructing the Trapezoidal Map, which is obtained by extending vertical walls from each endpoint upward and downward until an input curve is reached or the wall extends to infinity. During the incremental construction, an auxiliary search structure, a directed acyclic graph (DAG), is maintained. It has one root and many leaves, one for every trapezoid in the trapezoidal map. Every internal node is a binary decision node, representing either an endpoint \(p\), deciding whether a query lies to the left or to the right of the vertical line through \(p\), or a curve, deciding if a query is above or below it. When we reach a curve-node, we are guaranteed that the query point lies in the \(x\)-range of the curve. The trapezoids in the leaves are interconnected, such that each trapezoid knows its (at most) four neighboring trapezoids, two to the left and two to the right. (Degeneracies, such as co-vertical endpoints are handled by the fact that we a lexicographic comparison is used. This implies that two co-vertical points produce a virtual trapezoid, which has a zero width.)
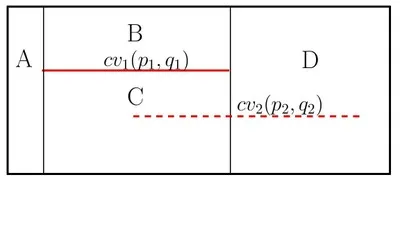
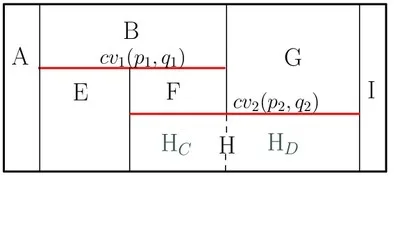
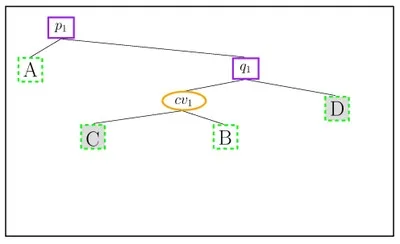
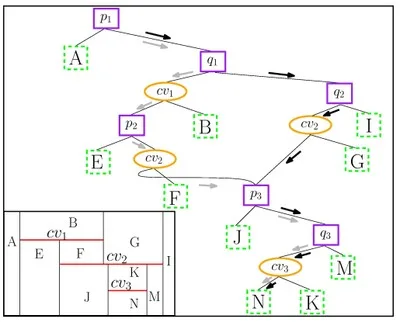
When a new \(x\)-monotone curve is inserted, the trapezoid containing its left endpoint is located by a search from root to leaf. Then, using the connectivity mechanism described above, the trapezoids intersected by the curve are gradually revealed and updated. The figure below illustrates the trapezoidal decomposition and the constructed DAG for two segments \(\text{cv}_1\) and \(\text{cv}_2\): (a) before and (b) after the insertion of \(\text{cv}_2\). The insertion of \(\text{cv}_2\) splits the trapezoids \(C\), \(D\) into \(E\), \(F\), \(H_C\) and \(G\), \(I\), \(H_D\), respectively. \(H_C\) and \(H_D\) are merged into \(H\), as they share the same top (and bottom) curves.
For an unlucky insertion order the size of the resulting data structure may be quadratic, and the longest search path may be linear. However, due to the randomization one can expect \(O(n)\) space, \(O(\log n)\) query time, and \(O(n \log n)\) preprocessing time.
Guaranteed Logarithmic Planar Point Location
One can build a data structure, which guarantees \(O(\log n)\) query time and \(O(n)\) size, by monitoring the size and the length of the longest search path \(L\) during the construction. The idea is that as soon as one of the values becomes too large, the structure is rebuilt using a different random insertion order. It is shown that only a small constant number of rebuilds is expected. However, in order to retain the expected construction time of \(O(n \log n)\), both values must be efficiently accessible. While this is trivial for the size, it is not clear how to achieve this for \(L\).
Is it possible to access \(L\) in constant time?
- It seems that \(L\) cannot be made constant-time accessible while retaining linear space, since each leaf would have to store a non-constant number of values, i.e., one for each valid search path that reaches it.
- Using the depth \(D\) of the DAG, which is an upper bound on \(L\) as the set of all possible search paths is a subset of all paths in the DAG. The depth \(D\) can be made constant-time accessible.
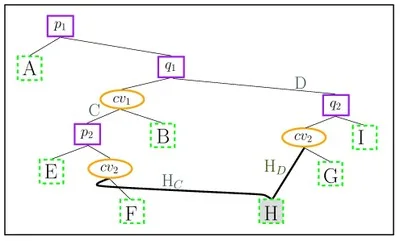
The figure below shows the DAG of the figure above after inserting a third segment. There are two paths that reach the trapezoid \(N\) (black and gray arrows). However, the gray path is not a valid search path, since all points in \(N\) are to the right of \(q_1\); that is, such a search would never visit the left child of \(q_1\). It does, however, determine the depth of \(N\), since it is the longer path of the two.
On the Difference of Depth and Longest Query Path
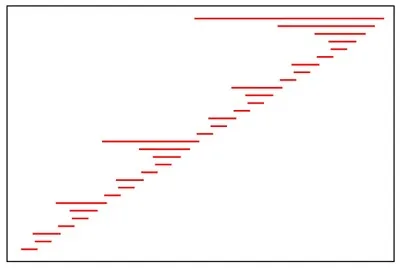
We use this observation to construct an example that shows that the ratio between \(D\) and \(L\) can be as large as \(\Omega(n / \log n)\), that is. for a given DAG its depth \(D\) can be linear while \(L\) is still logarithmic. In our paper we present a recursive construction that achieves such an \(O(n / \log n)\) ratio of \(D\) and \(L\), given in the figure below. We also show that this bound is tight (proof can be found in in the full version of the paper).
Such a DAG would trigger an unnecessary rebuild. It is thus questionable whether one can still expect a constant number of rebuilds when relying on \(D\).
Our experiments, which are fully described in the Appendix of the full version of the paper [link], show that in practice the two values hardly differ, indicating that it is sufficient to rely on \(D\). However, a theoretical proof to consolidate this is still missing.
Efficient preprocessing solutions for the static scenario
We present two efficient preprocessing solutions for the static scenario, where all segments are given in advance. Both solutions use the random incremental construction algorithm that monitors the size on the fly and runs in expected \(O(n \log n)\) time. After the construction, an algorithm that verifies that \(L\) is logarithmic is used. In the first solution we use an algorithm that recurs over the constructed DAG, for which we can only prove expected \(O(n \log^2 n)\) preprocessing time. The second solution uses the arrangement \(A(T)\) of all trapezoids created during the construction of the DAG (including intermediate ones that are later split by new segments). The key to the improved algorithm is an observation by Har-Peled: The length of a path in the DAG for a query point \(p\) is at most three times the depth of \(p\) in \)A(T)\), that is, at most three times the number of all trapezoids (including intermediate ones) that cover \(p\). The total preprocessing time achieved by the second solution is expected \(O(n \log n)\).
Acknowledgement
The authors thank Sariel Har-Peled for sharing his observation with them, which is essential to the expected \(O(n \log n)\) time algorithm for producing a worst-case linear-size and logarithmic-time point-location data structure.
Implementation
The new implementation for the trapezoidal-map random incremental construction for point location algorithm for CGAL arrangements is part of the latest CGAL release (4.1).
A comparison to CGAL Landmarks point location for arrangements can be found in the Appendix of the full version of the paper [link].
