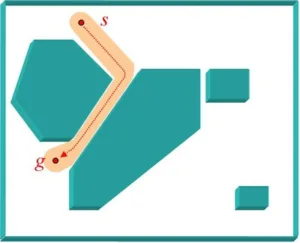
The motion-planning problem, involving the computation of a collision-free path for a moving entity amidst obstacles, is a central problem in fields like Robotics and Game Design. In this project we study the problem of planning high-quality paths.
A high-quality path should have some desirable properties: it should be short, avoiding long detours—and at the same time it should stay at a safe distance from the obstacles, namely it should have clearance.
We suggest a quality measure for paths, which balances between the above criteria of minimizing the path length while maximizing its clearance. We analyze the properties of optimal paths according to our measure, and devise an approximation algorithm to compute near-optimal paths amidst polygonal obstacles in the plane.
We also apply our quality measure to corridors. Instead of planning a one-dimensional motion path for moving entity, it is often more convenient to let the entity move in a corridor, where the exact motion path is determined by a local planner. We show that planning an optimal corridor is equivalent to planning an optimal path with bounded clearance.
Illustrations
|
|
|
|