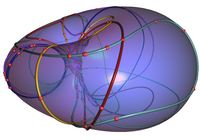
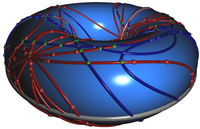
We introduce a general framework for processing a set of curves defined on a continuous two-dimensional parametric surface, while sweeping the parameter space. We can handle planes, cylinders, spheres, tori, and surfaces homeomorphic to them. A major goal of our work is to maximize code reuse by generalizing the prevalent sweep-line paradigm and its implementation so that it can be employed on a large class of surfaces and curves embedded on them. We have realized our approach as a prototypical CGAL package. We present experimental results for two concrete adaptations of the framework for: (i) arrangements of arcs of great circles embedded on a sphere, and (ii) arrangements of intersection curves between quadric surfaces embedded on a quadric.
The Topology-Traits Concept
In previous CGAL versions, planar arrangements used to be represented by the Arrangement_2 class template. This template has two parameters: the first is a geometry-traits class, which must be a model of the geometry-traits model, and the other is a class that represents a DCEL structure.
We now introduce a class template named Arrangement_on_surface_2, which represents an arrangement on an arbitrary surface. For backward compatibility, the geometry-traits class maintains the same interface. However, its predicates related to x and y should interpreted in the two-dimensional parameter space that defines the surface. The second template parameter is a topology-traits class, which defines the specific manner the arrangement is represented as a DCEL structure. We next give a more detailed description on the requirements from the topology-traits class.
First, the topology-traits class must define a nested Dcel type, which corresponds to the DCEL class used to represent the arrangement. In addition it must define visitors that perform certain tasks. The most important visitors are:
- Construction sweep-line visitor
- A sweep-line visitor class that can construct the arrangement of a set of curves from scratch.
- Insertion sweep-line visitor
- A sweep-line visitor class that can insert a set of curves into a non-empty arrangement.
- Overlay sweep-line visitor
- A sweep-line visitor class that constructs a new arrangement corresponding to the overlay of two input arrangements.
- Insertion zone visitor
- Used to insert a single curve into an existing arrangement by computing its zone. Like the sweep-line algorithm, the zone-computation algorithm is also implemented in a generic fashion and its output is determined by a visitor class.
The fact that the visitor classes are defined by the topology-traits classes makes it possible to support generic functions that operate on the Arrangement_on_surface_2 class. For example, the function insert_curves(arr, begin, end) accepts an arrangement instance arr and a range of curves defined by [begin, end). If the arrangement is empty, it uses the construction sweep-line visitor to sweep over the input curves and construct their arrangement. Otherwise, it uses the insertion sweep-line visitor to insert them into the existing arrangement.
There are usually several alternatives for the actual DCEL representation of an arrangement on a specific surface.
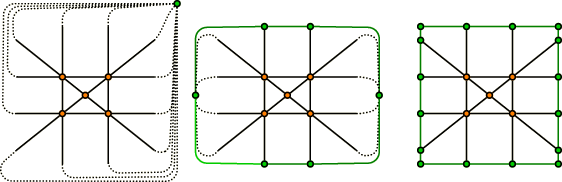
The topology-traits class encapsulates the actual DCEL representation of the arrangement. It provides access to the DCEL class, such that the Arrangement_on_surface_2 class can directly update DCEL records with no boundary conditions (i.e., all vertices and edges related to points and curves in the augmented parameter space). The topology-traits class is however responsible for handling the DCEL records that represents the surface boundaries: infinity, curves of discontinuity (identification), and singularity (contraction) points. To do so, it provides the following functionality:
- Initialize
- Construct a DCEL structure that represents an empty arrangement.
- Place boundary vertex
- Locate the DCEL vertex to which a given curve object with a boundary condition will be assigned, if existing. Otherwise it returns NULL.
- Notify on boundary vertex creation
- This function is used to notify the topological traits that a new DCEL vertex has been created which carries a boundary condition. This way it is possible to keep the internal objects of the topological traits up-to-date.
- Locate around boundary vertex
- For a given DCEL vertex, this functions returns the predecessor half-edge which identifies where to insert a given curve with a boundary condition. If may return NULL, if there is no such.
- Is redundant
- Determine whether a given vertex with a boundary condition becomes redundant. For example, a vertex that lie on a fictitious halfedge becomes redundant after one of its non-fictitious incident halfedges is deleted (typically it is only incident to two fictitious halfedges), or consider the case where a vertex representing a contraction point becomes isolated.
- Remove redundant vertex
- Remove a redundant vertex from the DCEL structure.
- Is perimetric path
- Determine whether a sequence of halfedges (given by first and last halfedge) forms a perimetric path, i.e., crosses an existing curve of identification an odd number of times.
- Boundaries of same face
- Check whether two given perimetric loops (each indicated by an halfedge) form outer boundaries of the same incident face.
Example
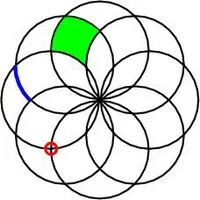
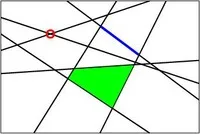
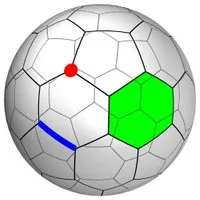
Given a collection \(C\) of curves on a surface, the arrangement \(A(C)\) is the partition of the surface into vertices, edges and faces induced by the curves of \(C\).
|
|
|
|
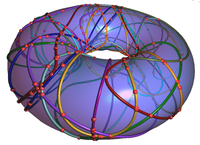
Further Example: Arrangements on ring Dupin Cylides
We provide a geometric and topologic traits class to compute arrangement on (parameterized) ring Dupin Cyclides induced by intersection of the cyclide with algebraic surfaces of any degree D. The family of Dupin cyclides contains as a special case the torus: Such an intersection is represented as real algebraic (plane) curve of bi-degree (2D,2D). CGAL’s experimental bivariate algebraic kernel provides the analysis of such curves. We use and extend it by asymptotic information about curves approaching infinity to define a proper geometric traits that reflects specialties when interpreting them with respect to the cylide’s parameter space. Our new topological traits provides the demanded operations to model the particularities of the genus-one reference surface. The implementation does not assume generic position. Our experiments show that the combinatorial overhead of the framework (choice of topology traits: planar versus cyclidean) does not harm the efficiency of the method and that the overall performance is strongly coupled to the efficiency of the implementation for arrangements of algebraic plane curves. Arrangements on tori also support applications, for example, in robot motion planning: The “all space” of a two-link planar robot arm is toroidal.
|
|
|
|