We present a new construction of approximate offset polygons whose boundaries consist of straight-line segments and circular arcs, and whose vertex coordinates are rational. The construction time depends on the number of vertices of the input polygonal shape and on the approximation tolerance.
See the details on the deconstruction of the approximate offsets.
Abstract
We devised and implemented a novel algorithm for the approximate construction of offset polygons. The exact offset of a polygonal shape whose vertex coordinates are rational, with rational offset radius, can have non-rational vertices. In contrast our new algorithm constructs for given polygonal shape \(P\), offset \(r\), and tolerance \(\epsilon\), an \(\epsilon\)-approximation of \(\text{offset}(P,r)\) whose vertex-coordinates are rational and that prefers circular arcs over piecewise-linear approximation where the exact offset also shows circular arcs.
The Goals
We give a novel \(\epsilon\)-approximation for \(\text{offset}(P,r)\) consisting of straight-line segments and circular arcs and denoted as \(\tilde{Q}\) that meets three conditions:
- \(H(\tilde{Q}, \text{offset}(P,r)) \leq \epsilon\) (where H denotes Symmetric Hausdorff Distance)
- The vertices of \(\tilde{Q}\) have rational coordinates (of bounded bitlength), and finally
- \(\tilde{Q}\) prefers a circular arc over a piecewise-linear approximation where the exact offset also shows a circular arc.
Goals 1 and 2, namely, producing a guaranteed approximation with rational vertex coordinates are particularly important when the offset polygon is the input to further or cascaded geometric computation. Goal (3) is useful for scenarios like NC milling.
The Algorithm
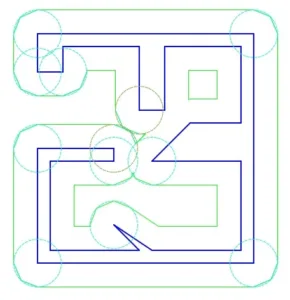
An offset \(r\) of a polygon \(P\) is defined as a Minkowski sum with a disk of radius \(r\): \(P \oplus D(r)\). We create a rational-vertex inner approximation of the disk by a polygon \(K\), that is the kgon’s vertices lie on the boundary of \(D(r)\), and and its edges are within its inner \(\epsilon\)-annulus. Notice that \(P \oplus K\) already achieves goals (1) and (2).
However we would like to receive a smother approximation with reduced number of vertices. To that purpose we ensure that slopes of \(K\) are unique, that is it is slope-disjoint with \(P\). Therefore it is easy to detect the sequences of \(K\)’s slopes in the \(P \oplus K\), and replace them with the corresponding circular arcs (that now do have rational endpoints). Such replacement is not straightforward, because it might not be possible to replace the \(K\)-slopes that were truncated (for non-convex \(P\)), or because such replacement can cause self-intersections in the resulting contour, or can create non-convex connections between circular arcs and segments of the contour, where the exact offset has smooth connections. We overcome these difficulties and produce rational vertex approximation that meets our goals.
Examples
The computation of the exact \(r-\epsilon\) inset (in orange) by current CGAL implementation (with CORE number types) took \(8.908\) sec.
The construction of the cascading approximate \(\epsilon\)-offset and the following \(r\)-inset (in green) with precision \(\delta = 10^{-1} \epsilon\) took only \(0.212\) sec. (Both constructions are done without the circular arc replacement step)

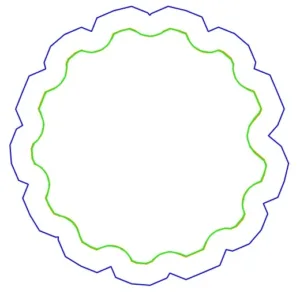
Our approximation (in cyan) compared to the existing implementation (in magenta) of the rational approximate offset in CGAL. The input polygon size is \(335\), \(\epsilon = 10^{-2} r\). The new approximation is smoother due to the nature of the involved algorithms, and in this case \((r/\epsilon < n)\) is computed faster (1.501 sec. vs 2.004 sec.)
