Deconstructing Approximate Offsets

We consider the offset-deconstruction problem: Given a polygonal shape \(Q\) with n vertices, can it be expressed, up to a tolerance ε in Hausdorff distance, as the Minkowski sum of another polygonal shape P with a disk of fixed radius? If it does, we also seek a preferably simple-looking solution shape \(P\); then, \(P\)’s offset constitutes an accurate, vertex-reduced, and smoothened approximation of \(Q\). We give an \(O(n \log n)\)-time exact decision algorithm that handles any polygonal shape, assuming the real-RAM model of computation. An alternative algorithm, based purely on rational arithmetic, answers the same deconstruction problem, up to an uncertainty parameter \(\delta\), and its running time depends on the parameter \(\delta\) (in addition to the other input parameters: \(n\), \(\epsilon\) and the radius of the disk). If the input shape is found to be approximable, the rational-arithmetic algorithm also computes an approximate solution shape for the problem. For convex shapes, the complexity of the exact decision algorithm drops to \(O(n)\), which is also the time required to compute a solution shape \(P\) with at most one more vertex than a vertex-minimal one. We present experimental results obtained with our implementation of the rational-arithmetic algorithm.
Additionally, we present a new construction of approximate offset polygons whose boundaries consist of straight-line segments and circular arcs, and whose vertex coordinates are rational. The construction time depends on the number of vertices of the input polygonal shape and on the approximation tolerance.

Illustrations

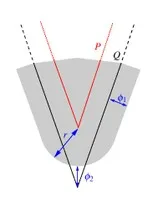
For a given \(Q\), the red \(P\) is a candidate summand whose exact \(r\)-offset is shaded.

(a) For a given \(\epsilon\), deconstruction is ensured iff \(\phi_1 \leq \epsilon\) and \(\phi_2 \leq \epsilon\). Otherwise, at least one, say \(\phi_1\), has to shrink, which, however, lets \(\phi_2\) grow (and vice-versa). Difficulty: a sharper angle lets \(\phi_2\) grow faster than \(\phi_1\) decreases.
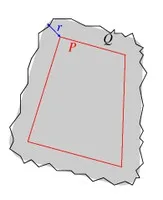
(b) Example where \(Q\) can be approximated by an \(r\)-offset of a P that has much fewer vertices than \(Q\).
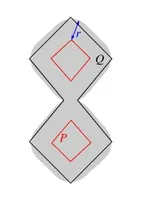
(c) Example where \(Q\) can be approximated by the \(r\)-offset of a disconnected shape \(P\).

The Decision Algorithm

1. Construct \(Q_{\epsilon} = \text{offset}(Q, \epsilon)\).
2. Construct \(\Pi = \text{inset}(Q_{\epsilon}, r)\). (\(\Pi\) is not generally a polygon, therefore it cannot serve as P in question, but it has to contain it).
3. Construct \(Q’ = \text{offset}(\Pi, r+\epsilon)\).
4. If \(Q \subseteq Q’\) then YES otherwise NO.

The Rational Arithmetic Algorithm Inner (and Outer) variant

1. Construct inner (outer) \(\delta\)-approximation of \(Q_{\epsilon}\). Let’s denote it \(S_1\).
2. Construct inner (outer) \(\delta\)-approximation of the \(r\)-inset of \(S_1\), i.e. inner (outer) \(2\delta\)-approximation of \(\Pi\). Let’s denote it \(S_2\).
3. Notice that \(S_2\) is a polygon, and in the inner variant \(S_2  \subseteq \Pi\), therefore it can serve as a valid \(P\), if the algorithm returns YES.
   Construct inner (outer) \(\delta\)-approximation of the \(r+\epsilon\)-offset of \(S_2\), i.e. inner (outer) \(3\delta\)-approximation of \(Q’\). Let’s denote it \(S_3\).
4. If \(Q \subseteq S_3\) then YES (UNDECIDED) otherwise UNDECIDED (NO).

Examples

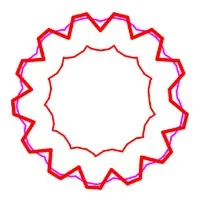
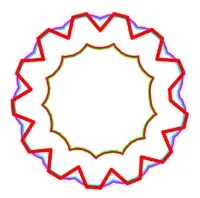
The wheel polygon (in bold) is the input for the two-sided decision procedure, that uses inner and outer rational arithmetic variants to get a certified YES/NO unswer. The input polygon is colored with traffic lights according to the algorithm decision (green for YES, yellow for UNDECIDED, red for NO). The pictures illustrate the influence of \(\epsilon\) and \(\delta\) on the algorithm outcome:

(a) Inner \(\Pi\) appears in green, inner \(Q’\) in cyan. It is easy to see that \(Q \subseteq Q’\), therefore \(r\)-offset of \(P=\Pi\) will be \(\epsilon\)-close to \(Q\).
(b) Outer \(\Pi\) appears in red, outer \(Q’\) in magenta. It is easy to see that \(Q \subseteq Q’\) is not true, therefore \(P\) with \(r\)-offset that is \(\epsilon\)-close to \(Q\) does not exist.
(c) \(Q\) is not in the inner \(Q’\) (cyan) and is completely inside outer \(Q’\) (magenta). The distance between inner \(Q’\) and outer \(Q’ \leq 6\delta\), therefore by decreasing \(\delta\) we can make it smaller and might be able to get a certified answer.
(d) With \(\delta d = 1/10 \epsilon < δc\), \(Q\) is not completely inside outer \(Q’\) (magenta), therefore is certified as not approximable.