This is a joint project with Geometrica.
Abstract
We introduce a new, efficient, and complete algorithm, and its exact implementation, to compute the Voronoi diagram of lines in three-dimensions. This is a major milestone towards the robust construction of the Voronoi diagram of polyhedra. Following the exact geometric computation paradigm, it is guaranteed that we always computes the mathematically correct result. The algorithm is complete in the sense that it can handle all configurations, in particular all degenerate ones. The algorithm requires \(O(n^{3+\epsilon})\) time and space, where n is the number of lines. The Voronoi diagram is represented by a data structure that permits answering point location queries in \(O(\log^2 n)\) expected time. The implementation employs the CGAL packages for constructing arrangements and lower envelopes on parametric surfaces together with advanced algebraic tools.
Bisectors
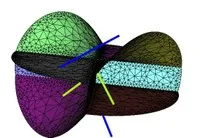
The bisector of two lines in space
|
|
|
|
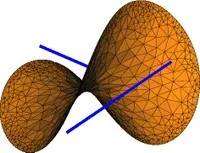
(a) Two generic lines—Hyperbolic paraboloid
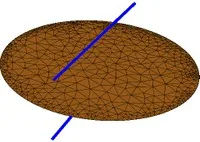
(b) Parallel lines—a plane
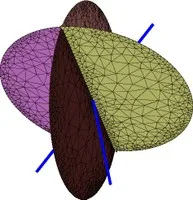
(c) Two intersecting lines—pair of orthogonal planes
More Diagrams
|
|
|
|
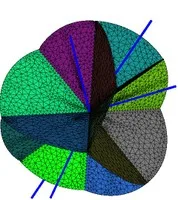
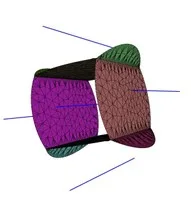
(a) Four lines intersecting at a single point
(b) Four lines—2 intersect and 2 others are parallel to each of them
(c) Five parallel lines
Open Question and Further Work
- A tight bound on the combinatorial complexity of the Voronoi diagram of \(n\) lines or line segments in \(\mathbb{R}^3\) is unknown; it is conjectured that the complexity is near-quadratic; the known lower bound is \(\Omega(n^2)\), but the best known upper bound is \(O(n^{3+\epsilon})\). In the case of lines with a fixed number \(c\) of orientations the upper bound was improved to \(O(c^4 n^{2+\epsilon})\). Thus, the open question is to close this gap.
- The exact computation is currently based on pure algebraic methods, which slows down the algorithm. Thus, it is necessary to introduce filters that avoid the use of exact arithmetic. Moreover, it would be useful to decrease the complexity of algebraic methods.
- So far it is only possible to compute the Voronoi diagram of lines. The next steps are to allow also line segments, points, triangles, and finally polyhedra.