Snap rounding (SR for short) is a well known method for transforming a planar arrangement of segments given in some arbitrary-precision coordinates into a fixed-precision representation. We extend the method to transforming an arrangement of geodesic arcs on the sphere. We present two approaches for solving the problem. A simple approach of enclosing the sphere in an isocube and projecting the arrangement onto its faces and a more complex approach that makes use of tools from Discrete Global Grid Systems (DGGS) to create a better approximation to the sphere. We also generalize the Guibas-Marimont proof of the topological properties preserved by the standard SR for segments in the plane; the generalization is needed for the DGGS approach. We present in detail the implementation of both approaches and give rounding results for both methods, obtained with our CGAL (Computational Geometry Algorithms Library) based implementation.
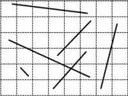
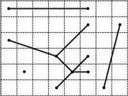
An arrangement of segments before (L) and after (R) snap rounding
Experimental Results
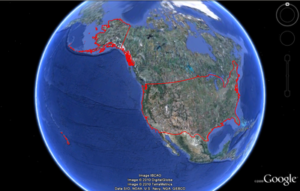
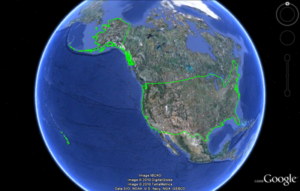
The snap rounding algorithm was tested on real world inputs. Specifically, we ran the algorithm on the border and roads of USA, where the results for the former are depicted below.
The input arrangement is illustrated in Figure (a). In (b) the resulting arrangement of the snap rounding algorithm is given. In (c) we zoom in on the San Diego bay area. The input, isocube and DGGS rounded arcs (red, green and blue, respectively) are very close such that there is no substantial difference between the three arrangements.
|
|
|
|