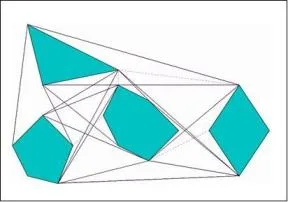
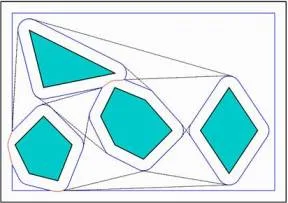
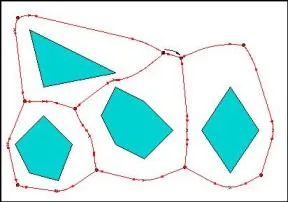
We introduce a new type of diagram called the \(\text{VV}(c)\)-diagram (the Visibility–Voronoi diagram for clearance \(c\)), which is a hybrid between the visibility graph and the Voronoi diagram of polygons in the plane. It evolves from the visibility graph to the Voronoi diagram as the parameter c grows from 0 to \(\infty\). This diagram can be used for planning natural-looking paths for a robot translating amidst polygonal obstacles in the plane. A natural-looking path is short, smooth, and keeps—where possible—an amount of clearance \(c\) from the obstacles. The \(\text{VV}(c)\)-diagram contains such paths.
We also propose an algorithm that is capable of preprocessing a scene of configuration-space polygonal obstacles and constructs a data structure called the VV-complex. The VV-complex can be used to efficiently plan motion paths for any start and goal configuration and any clearance value \(c\), without having to explicitly construct the \(\text{VV}(c)\)-diagram for that \(c\)-value.
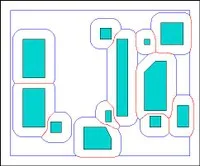
The preprocessing time is \(O(n^2 \log n)\), where \(n\) is the total number of obstacle vertices, and the data structure can be queried directly for any c-value by merely performing a Dijkstra search. We have implemented a CGAL-based software package for computing the \(\text{VV}(c)\)-diagram in an exact manner for a given clearance value, and used it to plan natural-looking paths in various applications.
Illustration
Visibility-Voronoi Diagrams with different clearance values
|
|
|
|