| We address a challenging problem in motion planning where robots must navigate through narrow passages in their configuration space. Our novel approach leverages optimization techniques to facilitate sliding and rolling movements across critical regions, which represent semi-free configurations, where the robot and the obstacles are in contact. Inspired by the human hand, our algorithm seamlessly traverses widely free regions, follows semi-free paths in narrow passages, and smoothly transitions between the two types. We specifically focus on complex scenarios such as tight assemblies, screw-like assemblies, and 3D wire puzzles, all requiring intricate simultaneous translations and rotations. Remarkably, these complexities also present computational challenges. The article provides four main contributions. First, we present a novel algorithm for coping with motion planning in tight settings. Second, we outperform state-of-the-art algorithms on certain (harder) problem types. Third, we present a rigorous analysis supporting the consistency of the algorithm. And fourth, we validate the quality of the generated plan by executing it in the real world using a robotic arm. The open source software and the accompanying videos are available at https://github.com/TAU-CGL/tr-rrt-public. This research sheds light on effective approaches to address motion planning difficulties in intricate 3D puzzle-like scenarios. |
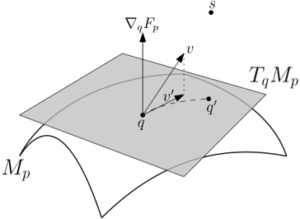 |
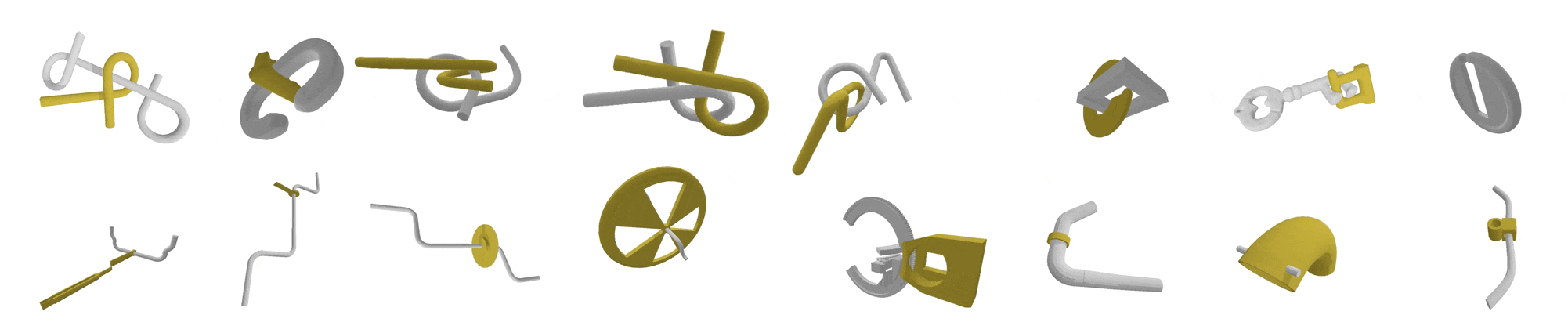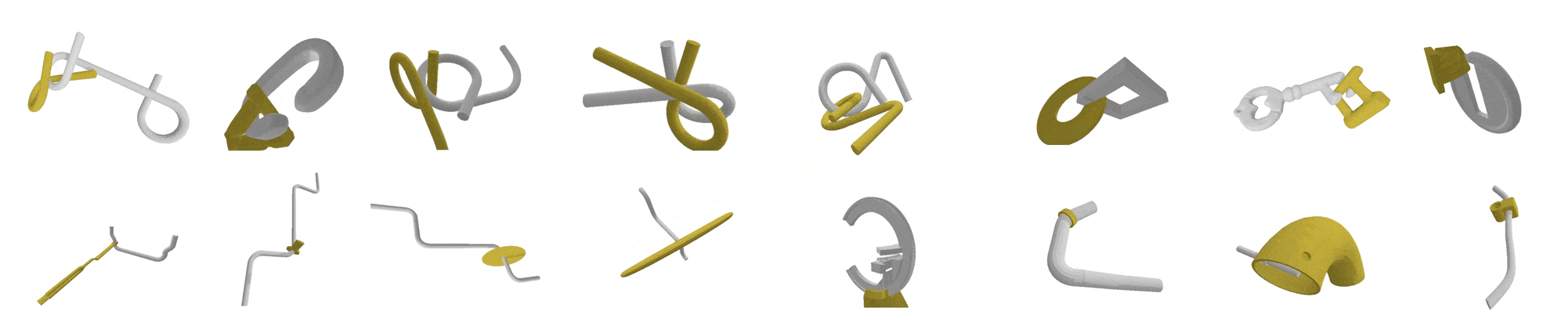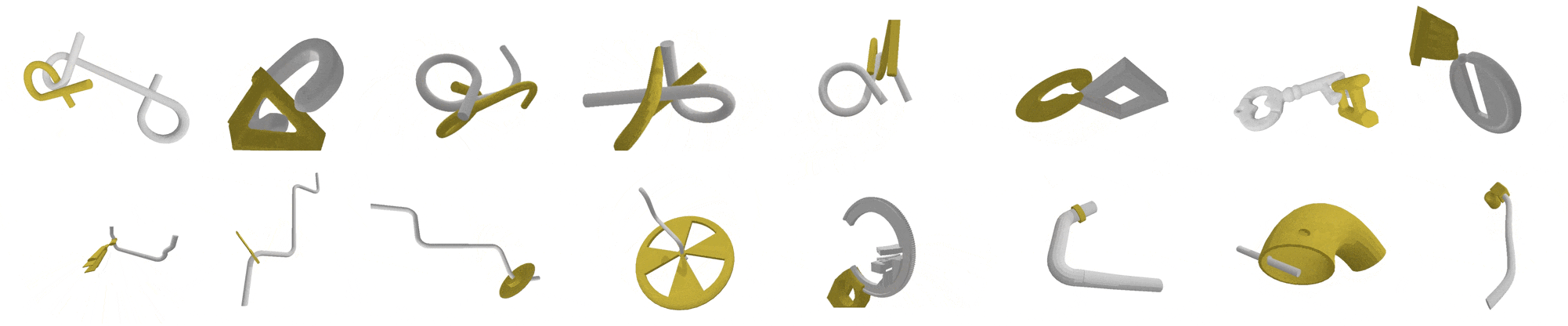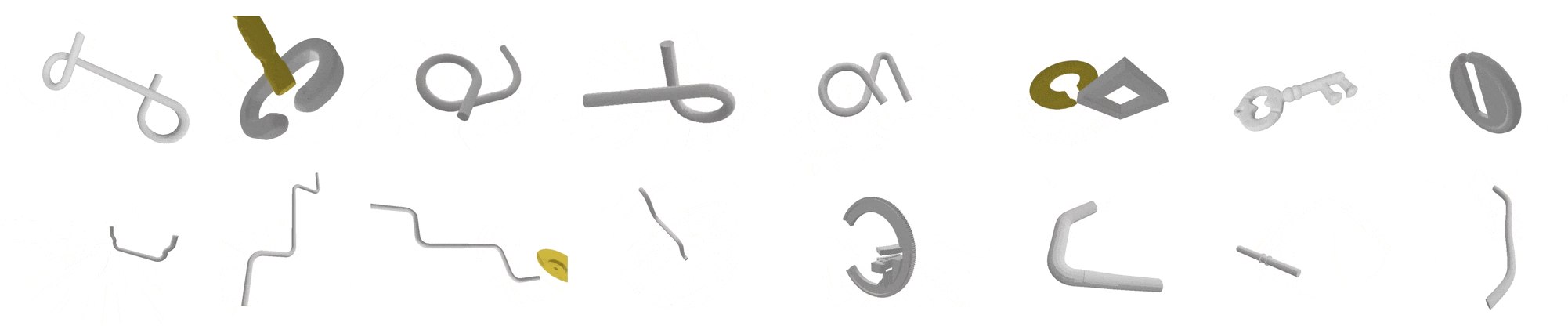 |
 |
 |
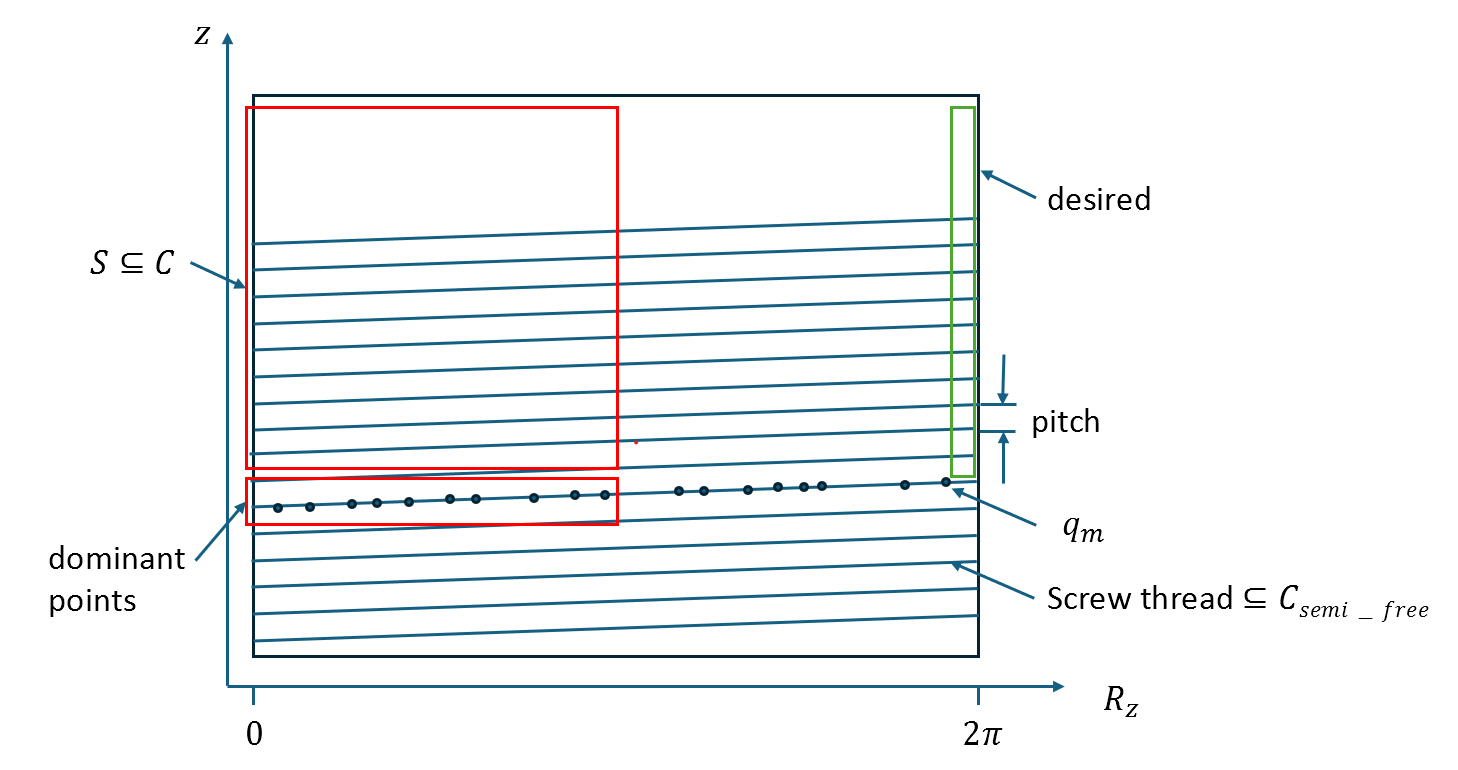 |
| In a recent work we show how by replacing the random samples in the search space with random samples close to the critical manifold, the search along the manifold improves dramatically, enabling to solve tight and very complex problems that have not been solved in the past. |  |
