An underlying structure in several sampling-based methods for continuous multi-robot motion planning (MRMP) is the tensor roadmap (TR), which emerges from combining multiple PRM graphs constructed for the individual robots via a tensor product. We study the conditions under which the TR encodes a near-optimal solution for MRMP—satisfying these conditions implies near optimality for a variety of popular planners, including dRRT*, and the discrete methods M* and CBS when applied to the continuous domain.
We develop the first finite-sample analysis of this kind, which specifies the number of samples, their deterministic distribution, and magnitude of the connection radii that should be used by each individual PRM graph, to guarantee near-optimality using the TR.
This significantly improves upon a previous asymptotic analysis, wherein the number of samples tends to infinity. Our new finite sample-size analysis supports guaranteed high-quality solutions in practice within finite time.
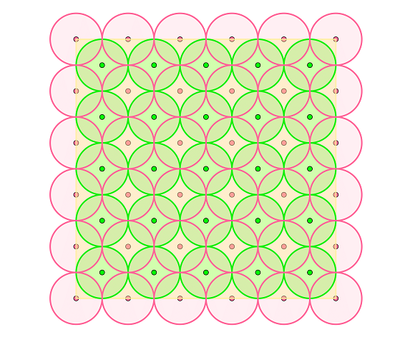
To achieve our new result, we first develop a sampling scheme, which we call the staggered grid, for finite-sample motion planning for individual robots, which requires significantly less samples than previous work. We then extend it to the much more involved MRMP setting which requires to account for interactions among multiple robots. Finally, we report on a few experiments that serve as a verification of our theoretical findings and raise interesting questions for further investigation.
