We present a general framework for implementing exact two-dimensional Voronoi diagrams of different classes of sites under various distance functions. The computation of the diagrams employs CGAL (the Computational Geometry Algorithm Library) for constructing envelopes of surfaces in 3-space, which implements a divide-and-conquer algorithm. A straightforward application of the divide-and-conquer approach for Voronoi diagrams yields algorithms, which are highly inefficient in the worst case. We show that through randomization, the expected running time is near-optimal (in the worst case). We also show how the framework can be used, together with existing tools from CGAL, to compute a minimum-width annulus of a set of disks in the plane. This requires the construction of two Voronoi diagrams of different types (one type of which appears not to have been investigated before) and of the overlay of the two diagrams. For all the diagrams discussed in the paper the implementation is exact and can handle degenerate inputs.
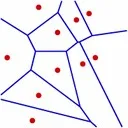
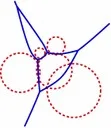
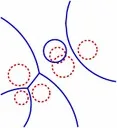
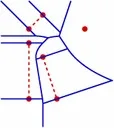
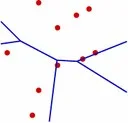
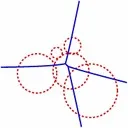
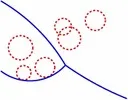
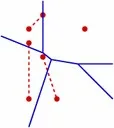
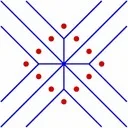
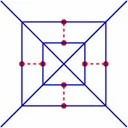
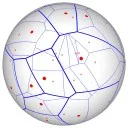
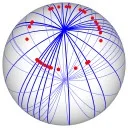
A variety of Voronoi diagrams can be computed using our robust framework. Some of these are depicted below. Sites are drawn in red and Voronoi edges are drawn in blue.
Nearest-Neighbor Voronoi Diagrams in the Plane
|
|
|
|
|
| (a) A standard Voronoi diagram (point sites with Euclidean metric). (b) An additively-weighted Voronoi(Apollonius) diagram with disk centers as sites and disk radii as weights. (c) A Mobuis diagram with disk centers as sites. The distance from every point on the boundary of a disk to its corresponding site is zero. (d) A Voronoi diagram of segments. * The sites in (b), (c), and (d) are displayed as dashed curves |
|||
Farthest-Neighbor Voronoi Diagrams in the Plane
|
|
|
|
|
| (a) A farthest point Voronoi diagram. (b) A farthest additively-weighted Voronoi diagram. (c) A farthest Mobius diagram. (d) A farthest Voronoi diagram of segments. |
|||
Degenerate Voronoi Diagrams in the Plane
|
|
|
|
| (a) A degenerate standard Voronoi diagram. (b) A degenerate additively-weighted Voronoi (Apollonius) diagram. (c) A degenerate Voronoi diagram of segments |
||
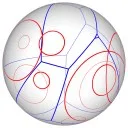
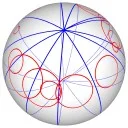
Voronoi Diagrams on the Sphere
|
|
|
|
|
| (a) The Voronoi diagram of 32 random points. (b) A highly degenerate case of Voronoi diagram of 30 point sites on the sphere. (c) The power diagram of 10 random circles. (d) A degenerate power diagram of 14 site on the sphere. |
|||
Supported Types of Voronoi Diagrams
The table below summarizes the types of diagrams that are currently supported by our implementation and their bisector classes.
| Name | Sites | Distance Function | Class Of Bisectors |
|---|---|---|---|
| Standard Voronoi diagram | points \(p_i\) | lines | |
| Power diagram | disks (with center \(c_i\) and radius \(r_i\)) | lines | |
| 2-point triangle-area Voronoi diagram | pairs of points \(\{p_i, q_i\}\) | pairs of lines | |
| Apollonius diagram | points \(p_i\) and weights \(w_i\) | hyperbolic arcs | |
| Möbuis diagram | points \(p_i\) with scalars \(\lambda_i\), \(\mu_i\) | |
circles and lines |
| Anisotropic diagram | points \(p_i\) with positive definite matrices \(M_i\), and scalars \(\pi_i\) | |
conic arc |
| Voronoi diagrams of linear objects | points, segments, rays, and lines | Eucledian distance | piecewise algebraic curves composed of line segments and parabolic arcs |
| Spherical Voronoi diagram | points on a sphere | geodesic distance | arcs of great circles (geodesic arcs) |
| Power diagram on a sphere | circles on a sphere | “spherical” power distance | arcs of great circles (geodesic arcs) |
FAQ
| Frequently Asked Questions | |
|---|---|
| Q |
How can I download and use the package? |
| A | The code is still experimental and will be available in the future. |
| Q |
Can the framework be use for producing power diagrams of weighted points in the plane? |
| A | Indeed, our framework allows the production of various types of Voronoi diagrams represented as CGAL arrangements. The main advantage of the framework is the easy (in terms of development) production of Voronoi diagrams rather than efficiency and speed of computation. The reason is that the framework relies on bisector construction and exact computation.
If you are looking for a fast and easy production of power diagrams, I refer you to the triangulation package of CGAL. The code can compute regular triangulations (which are the dual to power diagrams) that can be then adapted to Voronoi diagrams using the Voronoi diagram adaptor. |
| Q |
Can the framework be use for computing weighted medial axis? |
| A | The framework allows the computation of Voronoi diagrams of segments by constructing the lower envelope of their distance functions. If the bisectors of the requested diagrams are quadratic curves in the plane then it is possible to adapt the segments diagram code to support weighted distances. |